to main chapter Research fields
The low temperature motion of hydrogen on solid metal surfaces displays some unexplained
experimental features. In the quantum diffusion regime more than nine orders of
magnitude difference between the diffusion rates on different metal surfaces have
been measured, the lowest diffusion rates being established in the low temperature
scanning tunnelling microscope. Furthermore telegraph-signal-like adsorption
site change, rather than Rabi oscillations predicted by Schroedinger equation
in 3+1 dimensions, is observed, signaling the breakdown of quantum mechanics in
3+1 dimensions.
Within the EQM theory, involving the entanglement of the adsorbate motion to gravitons
in high-dimensional spacetime (11D), these problems are resolved. Soft local
massive gravonons, induced in the presence of the adsorbate, determine the time
scale for surface diffusion. The gamma-eta-model is used for the evaluation of
the soft gravonon modes. Weak and local entanglement of the adsorbate motion with
a nearly degenerate graviton continuum of high density of states are the conditions
for the telegraph-signal-like time development of adsorption site change. In contrast
to the Copenhagen interpretation of quantum mechanics, this apparent ''classical''
behaviour of the adsorbate in 3+1 dimensional spacetime is the result of the solution
of Schroedinger's time dependent equation in high-dimensional spacetime.
The theory provides values for the coupling strength and the geometry of the adsorbate-metal
complex in the transient state of the deformation resonance in which entanglement
to gravonons yields the experimental diffusion rates.
The geometry of the deformation resonance of the hydrogen atom on the metal surface
is in exceptionally good agreement with ab initio electronic structure calculations
for the same adsorption geometries, having in mind the strong distance dependence
of the results in 11D-theory and the fact that the two theories have no contact
points at all.
Entanglement between the adsorbate motion with environmental fields at very low temperatures
cannot be achieved in 3+1 dimensions by the common excitations (phonons, tomonagons,
etc.). If entanglement with the environment plays a role in these experiments,
the environmental excitations have to be gravitons in D+1 dimensional spacetime
(D=8,9,10,11).
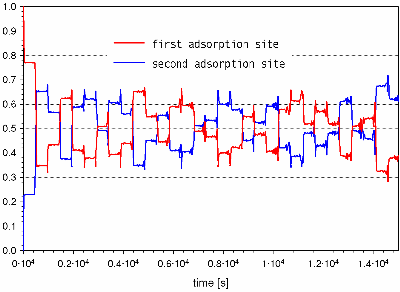
Changes of the squared projection of the world wave function on the initial state
with the adsorbate on site 1 of a two-site model with time. Telegraph-signal-like
site changes occur at time intervals, determined by the lifetime, i.e. the energy,
of the entangled soft gravonon modes.
D. Drakova and G. Doyen, J. Phys.: Conf. Series 442, 012049 (2013).
